Bài 5: Biểu diễn đồ thị

Tham khảo Video sau đây :

1.Biểu diễn bằng danh sách kề

Đồ thị vô hướng

Đỉnh	Các đỉnh kề
a	b,e
b	a,c
c	b,d,e
d	c,e
e	a,d,c

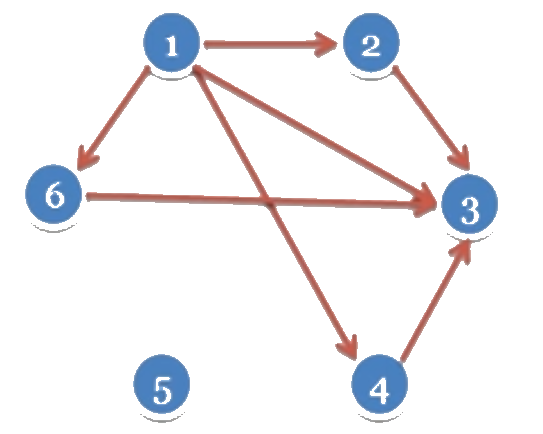
Đồ thị có hướng

Đỉnh đầu	Đỉnh cuối
1	2,3,4,6
2	3
3
4	3
5
6	3

2.Biểu diễn bằng ma trận kề

• Giả sử G=(V,E) trong đó V={v₁,v₂,..}, |V| = n

• Ma trận kề A của G là một ma trận 0-1 cấp mₓn có phần tử aᵢⱼ (dòng i và cột j) bằng 1 nếu vᵢ và vⱼ kề nhau và bằng 0 nếu vᵢ và vⱼ không kề nhau

Ví dụ 1

	a	b	c	d	e
a	0	1	0	0	1
b	1	0	1	0	0
c	0	1	0	1	1
d	0	0	1	0	1
e	0	1	1	1	0

💡 MẸO

Đối xứng nhau qua đường chéo chính

Số cạnh = (tổng hết số trong ma trận) / 2

Ví dụ 2

	1	2	3	4	5	6
1	0	1	1	1	0	1
2	0	0	1	0	0	0
3	0	0	0	0	0	0
4	0	0	1	0	0	0
5	0	0	0	0	0	0
6	0	0	1	0	0	0

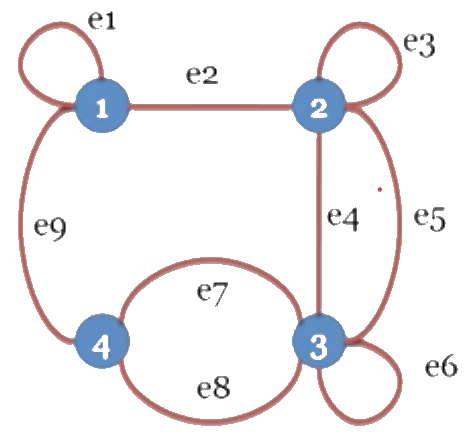
Ví dụ 3

	1	2	3	4
1	1	1	0	1
2	1	1	2	2
3	0	2	1	2
4	1	0	2	0

💡 MẸO

Với những ma trận vòng thì các định n-n là 1 (để ý đường chéo chính)

3.Biểu diễn bằng ma trận liện thuộc

• Giả sử G=(V,E), trong đó

  • V = {v₁,v₂,...}, |V| = n

  • E = {e₁,e₂,...}, |E| = e

• Ma trận liên thuộc M của G là một ma trận 0 tới 1 kích thước nₓe có phần tử aᵢⱼ (dòng i và cột j)

  • bằng 1 nếu cạnh eⱼ nối với đỉnh vᵢ

  • bằng 0 nếu cạnh eⱼ không nối với đỉnh vᵢ

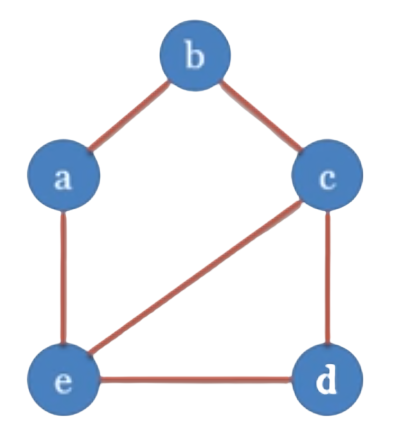
Ví dụ 1

	e1	e2	e3	e4	e5	e6
a	1	0	1	0	0	0
b	1	1	0	0	0	0
c	0	1	0	1	0	1
d	0	0	0	1	1	0
e	0	0	1	0	1	1
	(a, b)	(b, c)	(a, e)	(c, d)	(d, e)	(c, e)

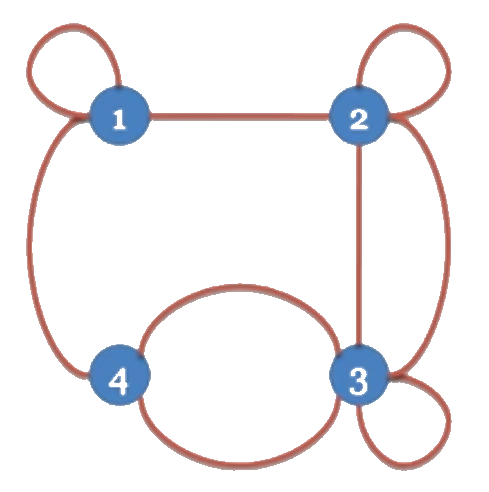
Ví dụ 2

	e1	e2	e3	e4	e5	e6	e7	e8	e9
1	1	1	0	0	0	0	0	0	1
2	0	1	1	1	1	0	0	0	0
3	0	0	0	1	1	1	1	1	0
4	0	0	0	0	0	0	1	1	1
	(1)	(2,3)	(2)	(2,3)	(2,3)	(3)	(3,4)	(3,4)	(1,4)

3.Bài tập