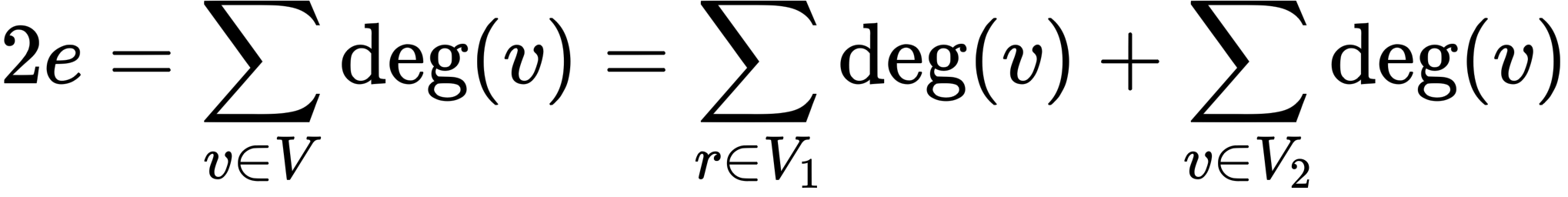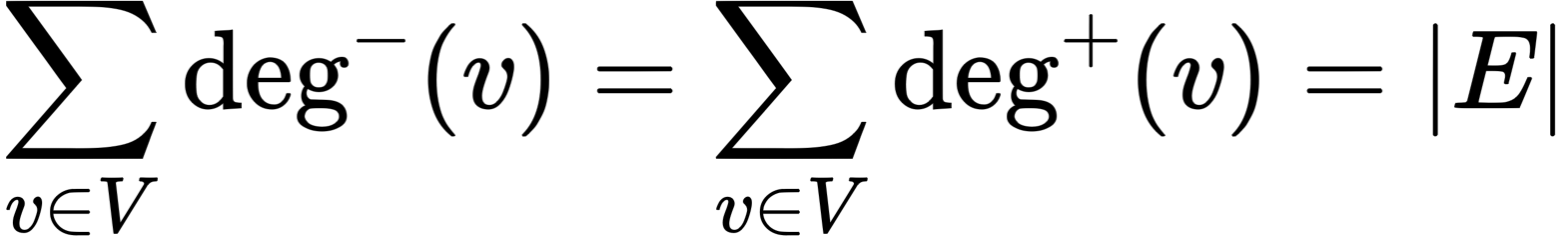Bài 3: Cạnh kề, đỉnh kề, bậc

Tham khảo Video sau đây :

1.Liên quan giữa cạnh và đỉnh

Khái niệm	Định nghĩa	Trong đó	Dễ hiểu
Kề	{u,v} là một cạnh của G trong đồ thị vô hướng	u và v là đỉnh G là đồ thị vô hướng	hai đỉnh nối với nhau bởi một cạnh gọi là kề
Liên thuộc	e={u,v}	e là cạnh nối u và v (u,v là đỉnh)	cạnh nối hai đỉnh với nhau gọi là liên thuộc
Điểm đầu nút	u và v		đỉnh còn được gọi là điểm đầu mút

Khi (u,v) là cạnh của đồ thị có hướng G

• u được gọi là nối tới v và v được gọi là nối từ u

• Đỉnh u được gọi là đỉnh đầu (initial vertex)

• Đỉnh v được gọi là đỉnh cuối (terminal hoặc vertex)

Cạnh e=(u,v) được gọi là đi từ đỉnh u tới đỉnh v (hoặc đi ra đỉnh u vào đỉnh v)

2.Bậc của đỉnh

Bậc (degree) của một đỉnh trên đồ thị vô hướng là số các cạnh liên thuộc với nó

💡 MẸO

• Riêng khuyên tại đỉnh được tính 2 lần cho bậc của nó.

• Ký hiệu : deg(v) (bậc của đỉnh v)

Ví dụ như sau :

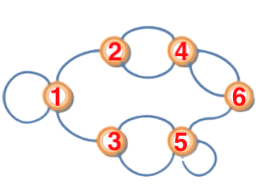
Đặt các đỉnh lần lượt từ 1 tới 6

==> Bậc của các định lần lượt như sau : 4, 3, 3, 4, 5, 3

a.Định lý bắt tay

Cho G=(V,E) là một đồ thị vô hướng có e cạnh, Khi đó :

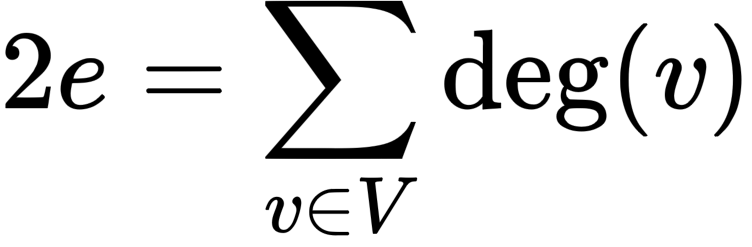
💡 VÍ DỤ

Có bao nhiêu cạnh trong đồ thị có 10 đỉnh và mỗi đỉnh có bậc bằng 7.

==> Mỗi đỉnh có bậc là 7 và có 10 đỉnh, vậy tổng số bậc là 70

Áp dụng công thức : 2e = 70 => e = 35 ==> Vậy có 35 cạnh

CHỨNG MINH ĐỊNH LÝ

Định nghĩa hàm f từ e x v tới {0,1,2...} , trong đó :

• f(e,v) = 1 nếu e có 2 đỉnh phân biệt và v là một trong 2 đỉnh đó

• f(e,v) = 2 nếu e là một khuyên và v là đỉnh của khuyên này

• f(e,v = 0) nếu v không phải là đỉnh thuộc cạnh e

  Trong đó : e là cạnh, v là đỉnh

==> Với cạnh e ∈ E bất kỳ, ta có

=>

Ta có : deg(v) =

=>

b.Định lý về số đỉnh bậc lẻ

Một đồ thị vô hướng có số lượng đỉnh bậc lẻ là một số chẵn

💡 MẸO

Không tồn một đồ thị vô hướng nào tổng số lượng đỉnh bậc lẻ là 1,3,5...

CHỨNG MINH ĐỊNH LÝ

Giả sử V1, V2 tương ứng là tập các đỉnh bậc chẵn và tập các đỉnh bậc lẻ của đồ thị vô hướng G=(V,E). Khi đó :

==> Không tồn tại đỉnh nào vừa nằm tập V1 và V2

Vì deg(v) là chẵn

3.Bậc vào và bậc ra

Trong đồ thị có hướng thì :

• bậc vào (in-degree) của đỉnh v, ký hiệu :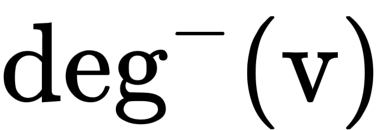

• Bậc ra (out-degree) của đỉnh v là số cạnh các đỉnh đầu là v, ký hiệu :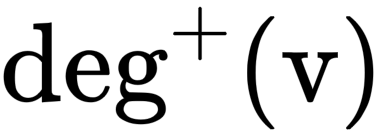

💡 MINH HỌA

---

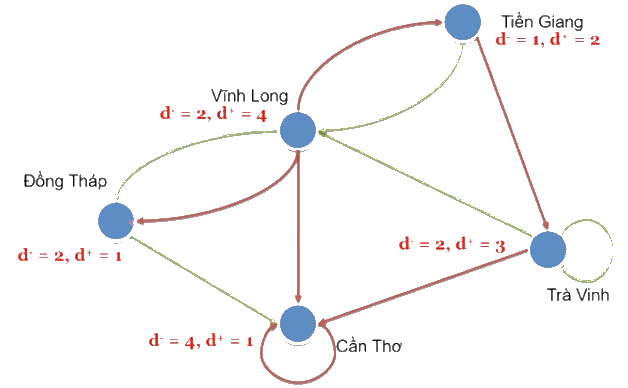
a.Định lý về số bậc đồ thị

Cho G=(V,E) là một đồ thị có hướng, Khi đó:

💡 GHI NHỚ

• Đỉnh treo (pendant vertex) là định có bậc bằng 1

• Đỉnh cô lập (isolated vertex) là đỉnh có bậc bằng 0

MINH HỌA

==> Trà vinh là đỉnh treo và Phú Quốc là đỉnh cô lập

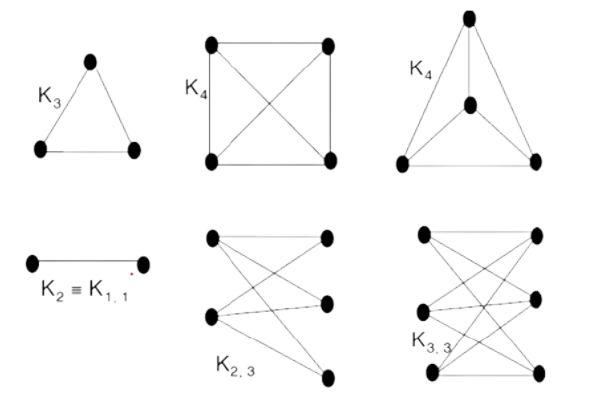
b.Một số đơn đồ thì đặc biệt

Đồ thị (Graph)	Định nghĩa	Ký hiệu	Mô hình
Đầy đủ (Complete)	là đồ thị chứa đúng một cạnh nối mỗi cặp đỉnh phân biệt	Kₙ (n đỉnh)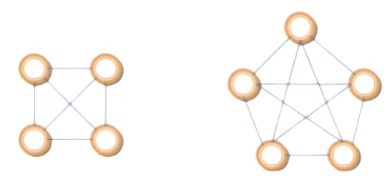
Chính quy (Regular)	là đơn đồ thị mà bậc của mọi đỉnh bằng nhau	Nếu bậc của các đỉnh là n gọi là n-chính quy	2-chính quy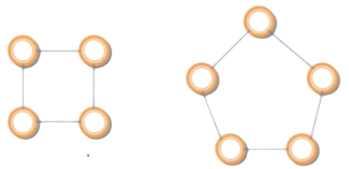 3-chính quy 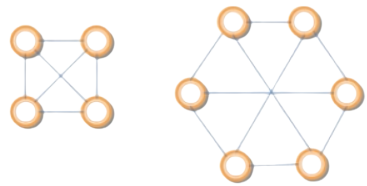4-chính quy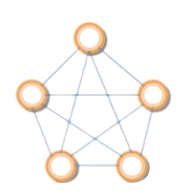
Vòng tròn (Circle)	là một đồ thị có n đỉnh và các cạnh	các đỉnh v₁,v₂..vₙ  các cạnh : {v₁,v₂}, {v₂,v₃}...{vₙ₋₁,vₙ} và {vₙ₋₁,vₙ}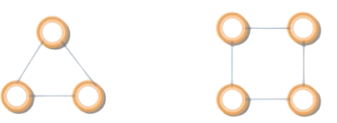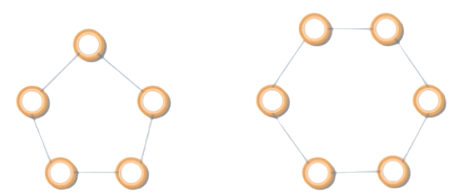
Phân đôi (Bipartite)	là đơn đồ thị có tập các đỉnh V có thể phân làm hai tập con rỗng, rời nhau	G có thể phân thành V₁ và V₂ sao cho mỗi cạnh của G nối một đỉnh của V₁ với một đỉnh của V₂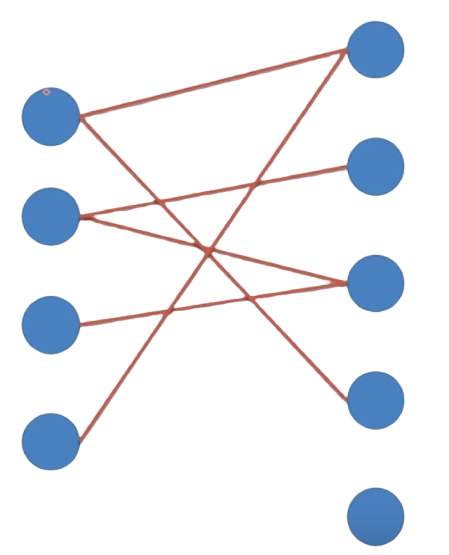
Phân đôi đầy đủ (Complete Bipartite)	là đồ thị có tập đỉnh được phân thành hai tập con có một cạnh thuộc	G có phân thành V₁ và V₂ có m đỉnh và n đỉnh cạnh giữa hai đỉnh thuộc tập con của đỉnh này và đỉnh thứ 2 thuộc tập con kia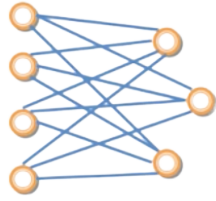

⚠️ GHI NHỚ

• Đồ thị đầy đủ tương đương với một đồ thị chính quy

• VD: Đồ thị K5 là 4-chính quy

VÍ DỤ

Sau đây là ví dụ của các dạng đồ thị trên :