Bài 4: Đồ thị đặc biệt

Tham khảo Video sau đây :

1.Đồ thị con và bộ phận

Khái niệm

• Đồ thị con (subgraph) của đồ thị G=(V,E) là đồ thị H=(W,F)

  Trong đó : W ⊆ V và F ⊆ E

• Đồ thị H là con của đồ thị G được gọi là đồ thị bộ phận (spanning subgraph) của G khi W = V

💡 MẸO

• Đồ thị con yêu cầu tập đỉnh và tập cạnh là tập con

• Đồ thị bộ phân yêu cầu chỉ có tập cạnh là tập con và tập đỉnh phải bằng nhau

⚠️ LƯU Ý

Đồ thị bộ phận là trường hợp đặc biệt của đồ thị con

==> Đồ thị bộ phận cũng là đồ thị con

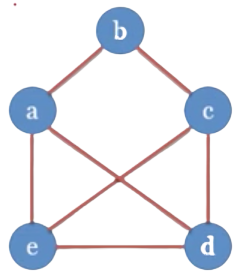
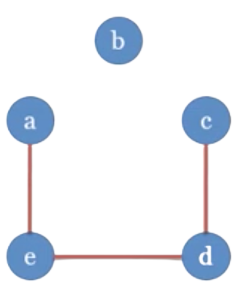
Ví dụ

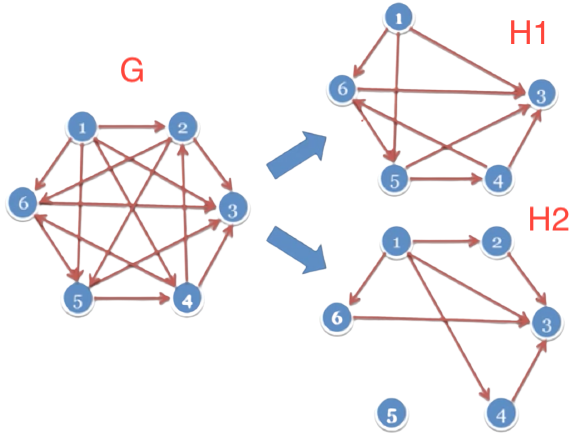
==> Đồ thị H1 là đồ thị con của G

Đồ thị H2 là đồ thị bộ phận của G

2.Bài tập

Câu 1

Cho G là đồ thị đơn, vô hướng có số đỉnh n > 3.

❓ Chứng minh G có chứa 2 đỉnh cùng bậc

💡 CÁCH GIẢI

• Giả sử có 1 đỉnh bậc 0 => đỉnh có bậc lớn nhất còn lại chỉ là n-2. Vậy các đỉnh có thể có bậc là 0..n-2

• Nếu không có đỉnh bậc 0 => các định có thể có bậc là 1,2...n-1

• Do vậy theo Dirichlet phải có ít nhất 2 đỉnh cùng bậc

Câu 2

Có thể tồn tại đồ thị đơn có 15 đỉnh, mỗi đỉnh có bậc bằng 5 hay không ❓

💡 CÁCH GIẢI

Không thể vì 15 (số đỉnh) x 5 (bậc) là một số lẻ.Điều trái với định lý bắt tay

Câu 3

Trong một buổi chiêu đãi, mọi người bắt tay với nhau.

❓ Chứng minh rằng tổng số người được bắt tay với một số lẻ người khác là một số chẳn

💡 CÁCH GIẢI

Chứng minh tương tự định lý số đỉnh bậc lẻ của đổ thị

Câu 4

Cách đồ thị sau có bao nhiêu cạnh ❓

• a) Kₙ

• b) Kₘ,ₙ

💡 CÁCH GIẢI

a. Số cạnh là =>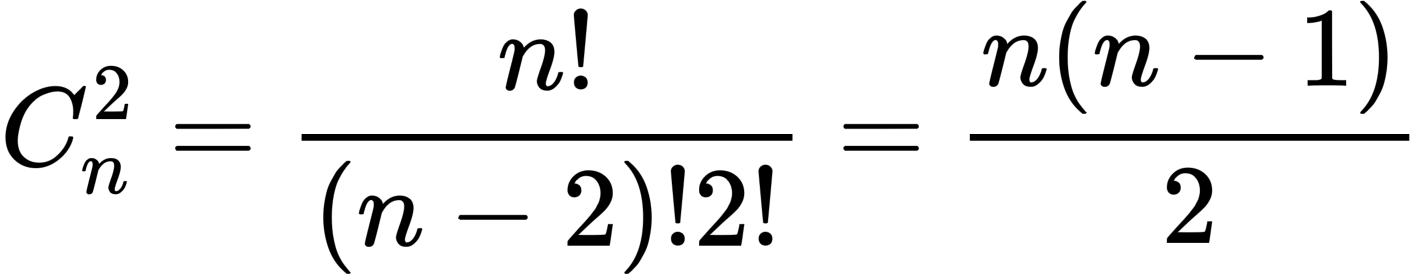

b. mₓn

Câu 5

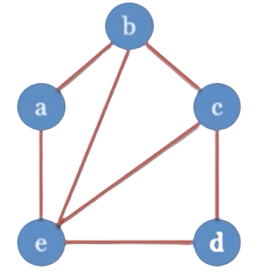
Đồ thị sẽ có bao nhiêu cạnh nếu có các đỉnh bậc 4,3,3,2,2

Vẽ đồ thị như vậy ❓

💡 CÁCH GIẢI

• Tổng số các bậc đỉnh của đồ thị là 4+3+3+2+2 = 14

• Vậy đồ thị này có 7 cạnh (nếu tồn tại đồ thị)

Câu 6

Có tồn tại đồ thị đơn chứa 5 đỉnh với các bậc sau đây

Nếu có hãy vẽ đồ thị đó ❓

💡 CÁCH GIẢI

• Đồ thị b,c,d không tồn tại vì (số đỉnh bậc lẻ là một số lẻ)

• Đồ thị a và e tồn tại như sau:

Đồ thị a :

Đồ thị e

Câu 7

Các đồ thị sau có phải đồ thị phân đôi không ❓

• a)

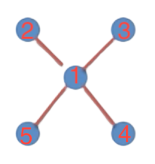
• b)

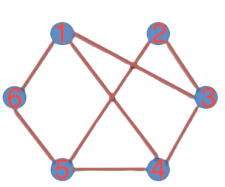
💡 CÁCH GIẢI

• a. Là đồ thị phân đôi vì :

  V1	V2
  1	2
  	3
  	4
  	5

• b. Không phải đồ thị phân đôi vì :

  V1	V2
  1	3
  2	4
  4	5

3.Đồ thị đẳng cấu

Khái niệm

Các đồ thị G₁ = (V₁,E₁) và G₂ = (V₂,E₂) là đẳng cấu nếu có hàm song ánh từ f từ V₁ lên V₂ sao cho các đỉnh u và v là liền kề trong G₁

Khi và chỉ khi : f(u) và f(v) là liền kề trong G₂ với mọi u,v trong V₁

==> Hàm f như vậy gọi là đẳng cấu

💡 VÍ DỤ

Đồ thị G₁ và G₂ là đẳng cấu với nhau :

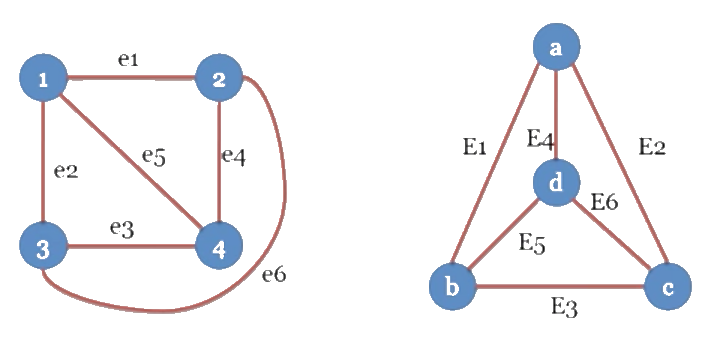
• f(1) = a, f(2) = b, f(3) = c, f(4) = d

• e₁ = E₁, e₂ = E₂

Chứng minh

Việc xác định đồ thị đẳng cấu hay không rất khó khăn

Vì để chứng minh là đẳng cấu, ta cần đưa ra quan hệ tương đương giữa 2 đồ thị này

Nhưng để chứng minh 2 đồ thị không đẳng cấp thì không quá khó khăn ==> Chỉ cần chỉ ra không có một tính chất đẳng cấu

💡 VÍ DỤ

Chứng minh 2 đồ thị sau không phải là đẳng cấu

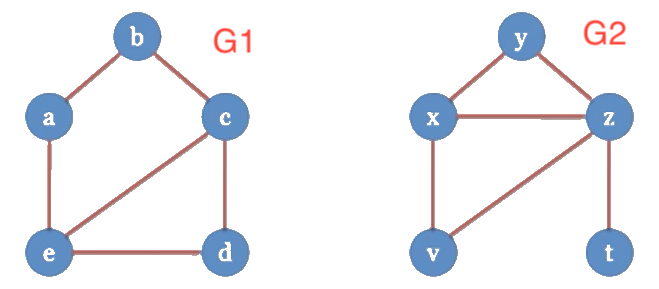
Chúng ta chỉ cần chỉ ra một trong những tính chất sau đây :

G1	G2
Có đỉnh treo (đỉnh t)	Không có đỉnh treo
Có 2 đỉnh bậc 3 (đỉnh e và d)	Có 1 đỉnh bậc 3 (đỉnh x)
Có 2 đỉnh bậc 2 kề nhau (đỉnh a và b)	Có 2 đỉnh bậc 2 nhưng không kề nhau

Còn nhiều nữa...