Bài thực hành 3

Trong bài này bạn cần nắm bắt các mục như sau :

• Tìm đường đi ngắn nhất bằng Dijkstra và bellman-Ford

• Kiểm tra chu trình âm và ứng dụng của đường đi ngắn nhất

💡 THƯ VIỆN

Sử dụng các thư viện sau:

#include <stdio.h>    // thư viện cơ bản của C
#include <stdbool.h>  // hỗ trợ true/false cho C
#include "list.h"     // thư viện cá nhân hỗ trợ danh sách

⇣ Download thư viện list.h

⚠️ LƯU Ý

Tất cả các đỉnh trong đồ thị bắt đầu từ 1 thay vì 0, nên hãy để ý rõ không thì sai !!!

Thuật toán Dijkstra

void dijksta(Graph G, int s, List *parrent, List *cost){
    bool mark[50];
    int u,v;
    for (u = 1; u <= G.n; u++){ //* khởi tạo mảng
        cost->Data[u] = 999;
        mark[u] = false;
        parrent->Data[u] = 0;
    }
    parrent->Size = cost->Size = G.n;

    cost->Data[s] = 0; //* đi từ đỉnh s, về đến đỉnh 
    parrent->Data[s] = -1; //* đỉnh bắt đầu không có parent 

    for (int i = 1; i <= G.n; i++){
        int min_pi = 999;
        for (int j = 1; j <= G.n; j++){
            //* Tìm đỉnh chưa duyệt có giá trị min_pi
            if(!mark[j] && cost->Data[j] < min_pi){
                min_pi = cost->Data[j];
                u = j;
            }
        }
        mark[u] = 1; //* đánh dấu đã duyệt xong đỉnh đó
        for (v = 1; v <= G.n; v++){
            if(G.A[u][v] != 0 && !mark[v]){
                int x = cost->Data[u] + G.A[u][v];
                if(x < cost->Data[v]){
                    cost->Data[v] = x;
                    parrent->Data[v] = u;
                }
            }
        }
    }
}

Thuật toán bellman-Ford

void bellmanFord(Graph G, int s,List *cost, List *parrent){
    for(int i=1; i<= G.n; i++){ // khởi tạo ban đầu
        cost->Data[i] = 999;
        parrent->Data[i] = 0;
    }

    cost->Size = parrent->Size = G.n;
    cost->Data[s] = 0; //có thể thay đổi
    parrent->Data[s] = -1; //có thể thay đổi

    for(int it = 1; it < G.n; it++){
        for(int k = 1; k <= G.m; k++){
            int u = G.edge[k].u;
            int v = G.edge[k].v;
            int w = G.edge[k].w;
            int x = cost->Data[u] + w;
            if(x < cost->Data[v]){
                cost->Data[v] = x;
                parrent->Data[v] = u;
            }
        }
    }
}

Mê cung số (nâng cao)

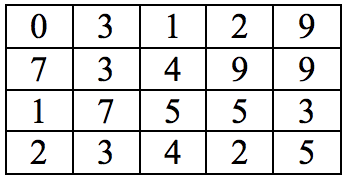
VÍ DỤ

💡 YÊU CẦU

• Xuất phát từ góc trái bên trên của ma trận (cụ thể là 0)

• Hãy tìm đường đi ngắn nhất từ vị trí xuất phát tới góc phải bên dưới của ma trận (cụ thể là 5)

==> Đường đi có chi phí thấp nhất cho ví dụ này là 24

int main(int argc, char const *argv[]){
    Graph G;
    makeNullGraph(&G);
    //freopen("dt.txt","r",stdin);
    int row,col;
    scanf("%d%d", &row,&col);
    G.n = row * col;
    init_Graph(&G, G.n);
    int M[MAX][MAX];
    for (int i = 0; i < row; i++){
        for (int j = 0; j < col; j++){
            scanf("%d",&M[i][j]);
        }
    }
    
    for (int i = 0; i < row; i++){
        for (int j = 0; j < col; j++){
            if(j + 1 == col){
                int x = i * col + j + 1;
                int y = (i+1) * col + j + 1;
                int t = M[i+1][j];
                add_edgeDirectionWeight(&G,x,y,t);
                G.m += 1;
            }
            else if(i + 1 == row){
                int x = i * col + j + 1;
                int y = i * col + (j+1) + 1;
                int t = M[i][j+1];
                add_edgeDirectionWeight(&G,x,y,t);
                G.m += 1;
            }
            else{
                int x = i * col + j + 1;
                int y1 = i * col + (j+1) + 1;
                int y2 = (i+1) * col + j + 1;
                int t1 = M[i][j+1];
                int t2 = M[i+1][j];
                add_edgeDirectionWeight(&G,x,y1,t1);
                add_edgeDirectionWeight(&G,x,y2,t2);
                G.m += 2;
            }            
        }
    }
    List cost; makeNullList(&cost);
    List parrent; makeNullList(&parrent);
    dijkstra(G,1,M[0][0],&parrent,&cost);
    
    printf("%d",cost.Data[G.n]);
    return 0;
}