Bài 9: Cây khung của đồ thị

Tham khảo Video sau đây :

1.Cây khung của đồ thị

LÝ THUYẾT

• Nếu đồ thị bộ phận T của đồ thị vô hướng liên thông, G=(V, E) là một cya6 thì khi đó cây T được gọi là cây khung (spanning tree) của đồ thị G

• Cây khung còn có tên gọi khác là cây phủ, cây bao trùm, cây tối đại.

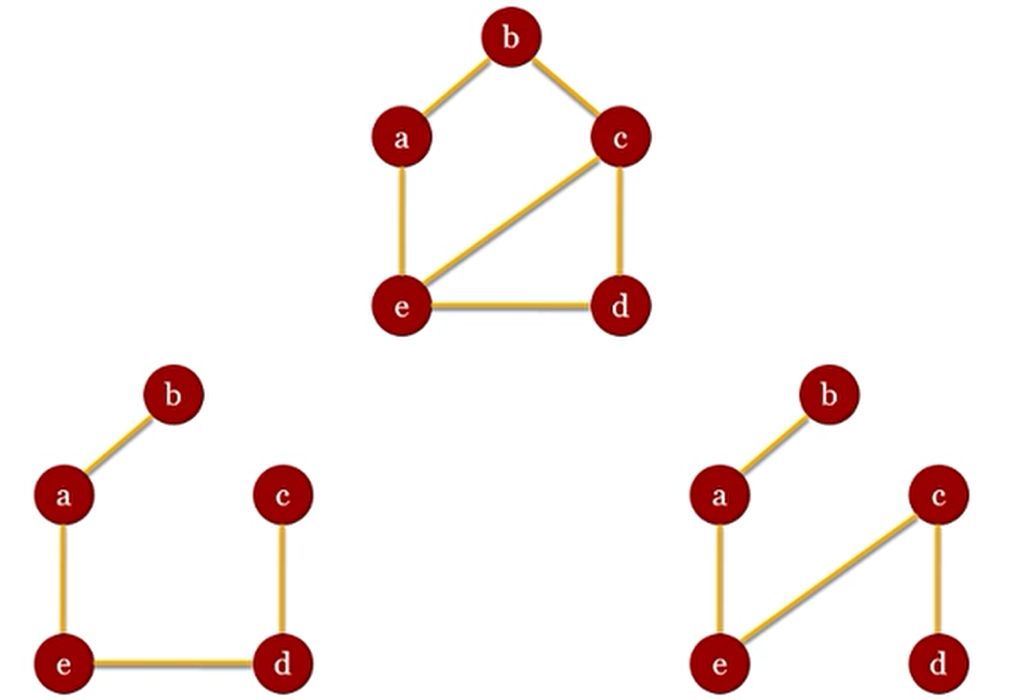
Ví dụ về cây khung

==> Đồ thị 2 và 3 là cây khung của đồ thị 1 vì nó là đồ thị bộ phận và không có chu trình

LƯU Ý

• Một đơn đồ thị là liên thông nếu nó là cây khung

• Định lý Borchart, Sylvester, Cayley ==> Số cây khung của đồ thị đầy đủ Kₙ là nⁿ⁻²

2. Cây khung nhỏ nhất lớn nhất

Cho G=(V, E) là đồ thị vô hướng, liên thông. Mỗi cạnh e thuộc E của đồ thị được gán một trọng số hay chi phí không âm, gọi là độ dài của cạnh đó.

CÔNG THỨC

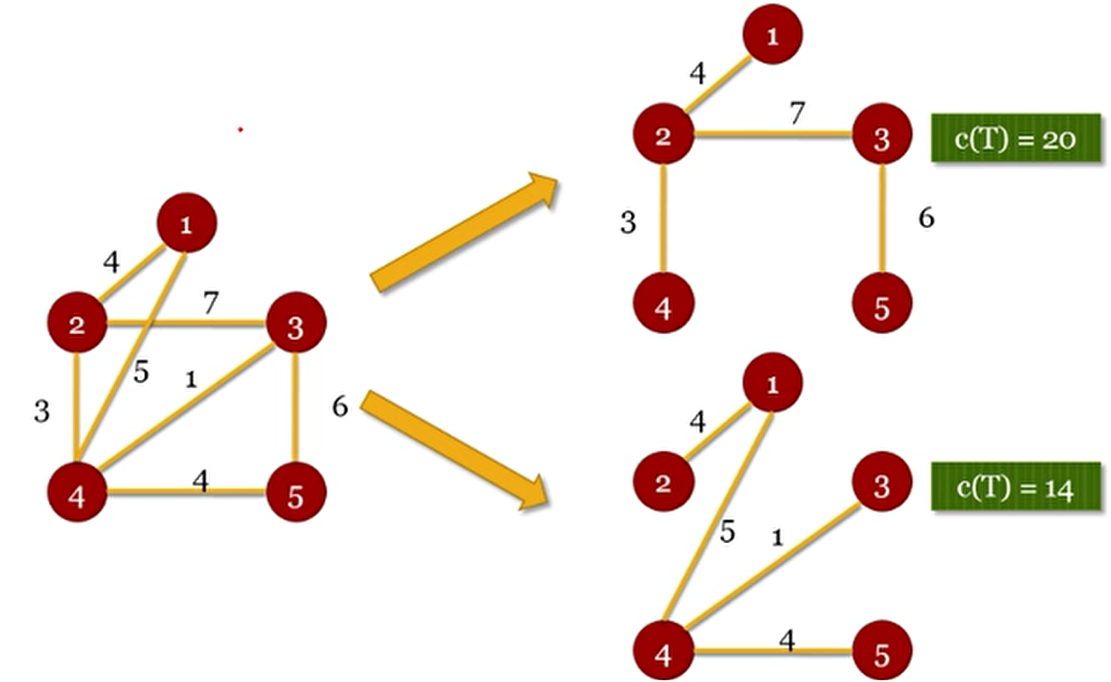
Giả sử T=(Vₜ, Eₜ) là cây khung của đồ thị G. Ta gọi độ dài C(T) của cây khung T là tổng độ dài các cạnh của nó

Ví dụ về đường đi của cây khung

3.Thuật toán tìm cây khung nhỏ nhất

GỒM 2 THUẬT TOÁN

Prim và Kruskal là hai thuật toán thông dụng để tìm cây khung nhỏ nhất

• Thuật toán Prim do Robert Prim vào năm 1957

• Thuật toán Kruscal do Joseph Kruskal phát minh vào năm 1956

Thuật toán Prim và Kruskal

Hãy theo dõi Video sau để hiểu thêm về thuật toán Prim và Kruskal

4. Ý tưởng thuật toán